leetcode weekly 132 to 136 - dp problems

weekly 132
(dp) 1027. Longest Arithmetic Sequence
Given an array A of integers, return the length of the longest arithmetic subsequence in A.

e.g. [20,1,15,3,10,5,8] = 4, [20,15,10,5] is the longest arithmetic subsequence.

ref: lee215' [Java/C++/Python] DP
https://leetcode.com/problems/longest-arithmetic-sequence/discuss/274611/JavaC%2B%2BPython-DP

// (CY 2nd attempt.) 2016 ms, faster than 51.45% 
// Memory Usage: 365.3 MB, less than 28.94%
int longestArithSeqLength(vector<int>& A) {
  const int n = A.size();
  // dp[i] = <Diff, Length> information start from A[0], and end with A[i]
  //
  // dp[i][diff] = arithmetic sequence length for 'diff',
  //               start from A[0], and end with A[i]
  //
  // Update order:
  // for i = 0..n-1
  //   for j = i+1..n-1
  //     dp[j][diff] = dp[i][diff] + 1
  vector<unordered_map<int, int>> dp(n);
  
  int longest = 0;
  for (int i = 0; i < n; ++i) {
    for (int j = i + 1; j < n; ++j) {
      const int d = A[j] - A[i];
      const int cnt = dp[i][d] + 1;
      dp[j][d] = cnt;
      longest = max(longest, cnt);
    }
  }

  return longest + 1;
}

// From Sampled commit - Without unordered_map
// 2380 ms, faster than 36.17% 
// Memory Usage: 8.7 MB, less than 92.28%
int longestArithSeqLength(vector<int>& A) {
  int count = 2;
  int ans = 2;
  for (int i = 0; i < A.size(); i++) {
    for (int j = i + 1; j < A.size(); j++) {
      int diff = A[j] - A[i];
      int target = A[j] + diff;
      count = 2;
      for (int k = j+1; k < A.size(); k++) {
        if (A[k] == target){
          target += diff;
          count++;
          ans = max(ans, count);
        }
      }
    }
  }
  return ans;
}

// From Sampled commit
// 24 ms, faster than 99.88%
// 26.5 MB, less than 80.83%
int longestArithSeqLength(vector<int>& A) {      
  int n = A.size();
  int pos[10001];
  memset(pos,-1,sizeof(pos));
  int d[n][n];
  memset(d,0,sizeof(d));
  int ret = 0;
  pos[A[0]] = 0;
  for(int i = 1; i < n; ++i) {
    for(int j = i + 1; j < n; ++j) {
      int prev = 2*A[i] - A[j];

      if (prev < 0 || prev > 10000 || pos[prev] == -1)
        continue;

      d[i][j] = d[pos[prev]][i] + 1;

      if (d[i][j] > ret)
        ret = d[i][j];
    }
    pos[A[i]] = i;
  }
  return ret + 2; 
}

weekly 134
(dp)(classical)(lcs) 1035. Uncrossed Lines
Given two integer arrays A and B.
We can draw a connecting line to connect two numbers from A, B if:

• A[i] == B[j]
• The line doesn't intersect with other connecting line.
• Each number can only belong to to one connecting line.

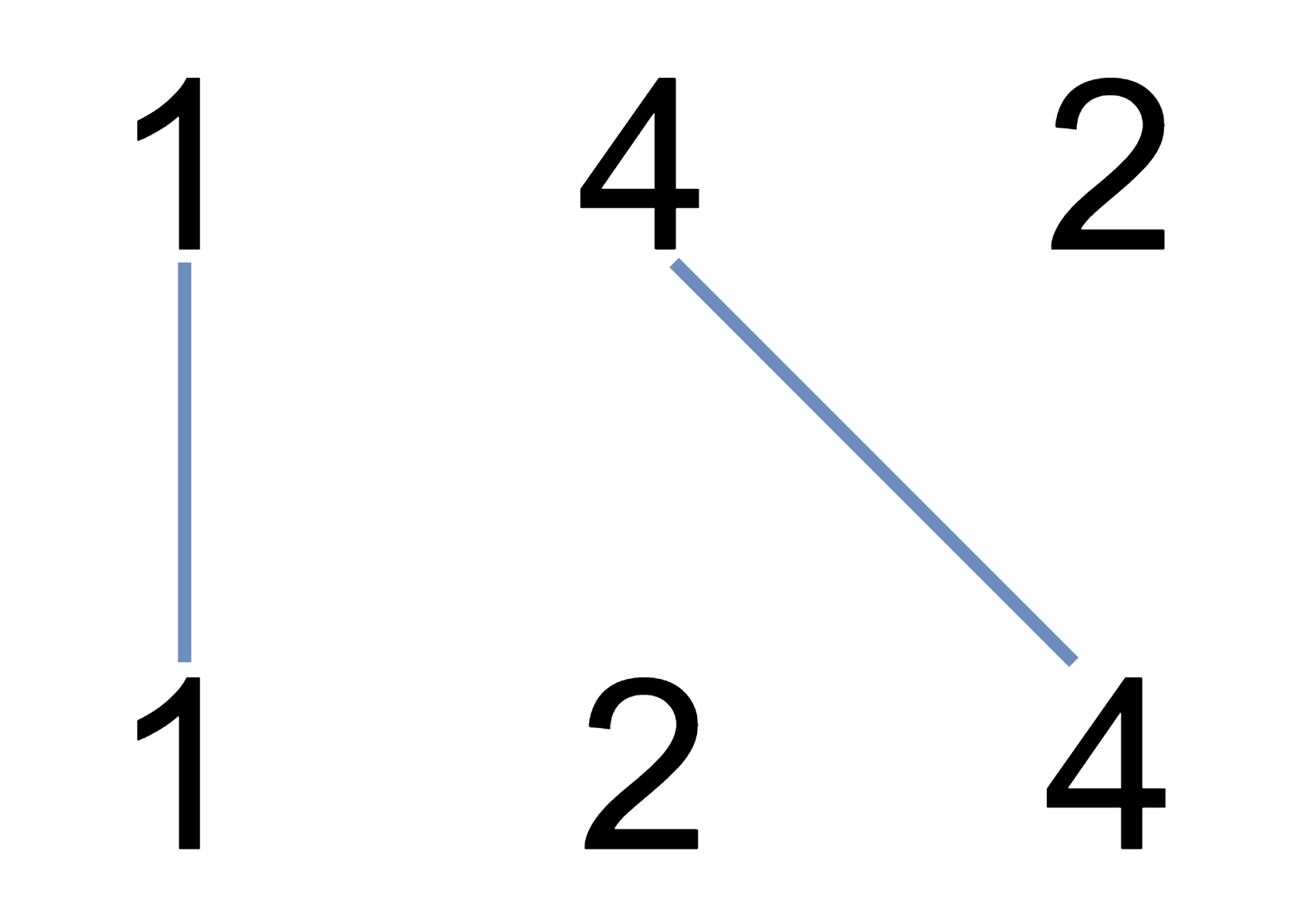
Return the maximum connecting line.

int maxUncrossedLines(vector<int>& A, vector<int>& B) {
  // Longest Common Subsequence.
  const int m = A.size() + 1;
  const int n = B.size() + 1;
  
  vector<vector<int>> dp(m, vector<int>(n));
  for (int r = 1; r < m; ++r)
    for (int c = 1; c < n; ++c)
      if (A[r-1] == B[c-1])
        dp[r][c] = dp[r - 1][c - 1] + 1;
      else
        dp[r][c] = max(dp[r - 1][c], dp[r][c - 1]);
  return dp[m - 1][n - 1];
}

weekly 135
(dp)(good) 1039. Minimum Score Triangulation of Polygon
Given a n-sided convex with vertices A[0], A[1], ... A[n - 1]

• Triangulate it into n - 2 triangles
• Each triangle has a score = A[i] * A[j] * A[k], i, j, k is the vertex of triangle.
• Return the smallest total score

See votrubac's explanation.
https://leetcode.com/problems/minimum-score-triangulation-of-polygon/discuss/286753/C%2B%2B-with-picture

// ref: neal_wu's contest solution
vector<vector<int>> dp;
int n;

int next(int idx) const { return (idx + 1) % n; }

int solve(int begin, int end, const vector<int> &A) {
  if (next(begin) == end)
    return 0;
  
  if (dp[begin][end])
    return dp[begin][end];
  
  int best = INT_MAX;
  for (int i = next(begin); i != end; i = next(i))
    best = min(best, 
               A[begin]*A[i]*A[end] + 
               solve(begin, i, A) + 
               solve(i, end, A));
  
  dp[begin][end] = best;
  return best;
}

int minScoreTriangulation(vector<int>& A) {
  n = A.size();
  dp.resize(n, vector<int>(n));
  int best = INT_MAX;
  for (int i = 0; i < n; ++i)
    for (int j = i + 1; j < n; ++j)
      for (int k = j + 1; k < n; ++k)
        best = min(best, 
                   solve(i, j, A) + 
                   solve(j, k, A) +
                   solve(k, i, A) +
                   A[i] * A[j] * A[k]);
  return best;
}

weekly 136
(dp) 1043. Partition Array for Maximum Sum
Example

Input: A = [1,15,7,9,2,5,10], K = 3
Output: 84
Explanation: A becomes [15,15,15,9,10,10,10]

Return the largest sum of the given array after partitioning.

int maxSumAfterPartitioning(vector<int>& A, int K) {
  // From lee215:
  // dp[i] record the maximum sum we can get considering A[0] ~ A[i]
  //
  // To get dp[i], we will try to change k last numbers separately to
  // the maximum of them, where k = 1 to k = K.
  const int n = A.size();
  int dp[n];
  dp[0] = A[0];
  
  for (int i = 1; i < n; ++i) {
    int maxSum = 0;
    int maxElem = 0;
    for (int j = 0; j < K; ++j) {
      if (i - j < 0)
        continue;

      maxElem = max(maxElem, A[i - j]);
      int curSum = maxElem * (j + 1);
      if (i - j - 1 >= 0)
        curSum += dp[i - j - 1];
        
      maxSum = max(maxSum, curSum);
    }
    dp[i] = maxSum;
  }

  return dp[n - 1];
}

// By neal_wu's contest solution
int maxSumAfterPartitioning(vector<int>& A, int K) {
    int N = A.size();
    vector<int> dp(N + 1, 0);

    for (int i = 1; i <= N; i++) {
        int most = 0;

        for (int j = i - 1; j >= max(i - K, 0); j--) {
            most = max(most, A[j]);
            dp[i] = max(dp[i], dp[j] + (i - j) * most);
        }
    }

    return dp[N];
}